We look at the first two terms and factor out the GCF (greatest common factor). Then we do the same process for the last two terms. Now, the (x+2) becomes a factor and then the remaining terms become the other factor of (3x^2+4). That is how we got the last line, but what I realized last week was that we actually factor out the GCF again. This time the GCF is (x+2) and then (3x^2+4) is what is left after you factor out the GCF, and this is how you get your two factors by grouping. I never realized that we were actually just factoring out the GCF again. I just always thought if the two ( ) were the same then they became one and then the remaining terms created the other factor.
This happens all the time in Math. The students follow a process, but they don't actually understand why they are doing it. Their secondary Math teachers just told them that it was done this way because they said so, or because that is how the book says to do it. As educators, we need to have our students discover processes of solving problems on their own. By doing so, they will be able to observe the steps in a more in depth manner, and they will be able to understand the why rather than just the process. I hope that as a future educator, I will be able to help my students make these connections and help them create a more conceptual understanding.
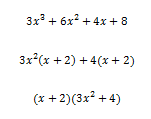
No comments:
Post a Comment